Logistic回归

分类Classification

$$
y \in {0, 1}
$$

自变量为0 1二值

将线性回归用于分类时，新增的单个参数可能并不会带来更多信息，但是能显著的改变模型状态。

Logistics回归

$$
h_\theta(x)=g(\theta^Tx),
g(z)=\frac{1}{1+e^{-z}}
$$

Sigmoid/Logistic function，在此呈现，其中的g(z)大概长如下这样

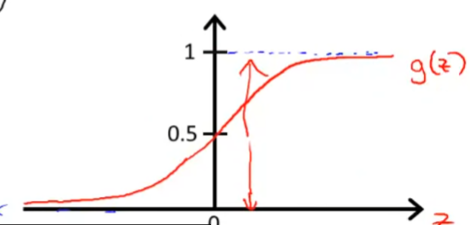
决定边界（Decision Boundary）

我们有：
$$
h_\theta(x)=g(\theta_0+\theta_1x+\theta_2x)
$$

如果要求最终结果=1，也就是g(z)内的值大于0，可得到一条直线
$$
\theta_0+\theta_1x+\theta_2x=0
$$
这条曲线分割了数据集，也就是我们的决定边界
$$
\begin{align*}& \theta = \begin{bmatrix}5 \newline -1 \newline 0\end{bmatrix} \newline & y = 1 ; if ; 5 + (-1) x_1 + 0 x_2 \geq 0 \newline & 5 - x_1 \geq 0 \newline & - x_1 \geq -5 \newline& x_1 \leq 5 \newline \end{align*}
$$
以上是一个例子

Cost Function

$$
J(\theta) = \frac{1}{m}\sum_{i=1}^m\frac12(h_\theta(x^{(i)})-y^{(i)})^2\newline
\frac12(h_\theta(x^{(i)})-y^{(i)})^2 = Cost(h_\theta(x^{(i)}),y^{(i)})^2
$$

以上是一个线性回归中我们用到的cost function

但在logistic回归中，这个曲线并不是一个凹面，不能很好的使用梯度下降，所以我们需要另一种cost function
$$
\begin{align*}& J(\theta) = \dfrac{1}{m} \sum_{i=1}^m \mathrm{Cost}(h_\theta(x^{(i)}),y^{(i)})
\newline & \mathrm{Cost}(h_\theta(x),y) = -\log(h_\theta(x)) ; & \text{if y = 1}
\newline & \mathrm{Cost}(h_\theta(x),y) = -\log(1-h_\theta(x)) ; & \text{if y = 0}\end{align*}
$$
由于这个分段函数并不是很优雅，我们有对其的简化版本
$$
\begin{align*} & h = g(X\theta)
\newline
& J(\theta) = \frac{1}{m} \cdot \left(-y^{T}\log(h)-(1-y)^{T}\log(1-h)\right) \end{align*}
$$

$$
\begin{align*} & Repeat ; \lbrace \newline & ; \theta_j := \theta_j - \frac{\alpha}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} \newline & \rbrace \end{align*}
$$